Il teorema di Bayes probabilità e inferenza

Introduzione al Teorema di Bayes

Il Teorema di Bayes è uno strumento fondamentale nella teoria della probabilità che ci permette di aggiornare le nostre credenze sulla base di nuove informazioni. Esso fornisce un modo formale per calcolare la probabilità di un evento, dato che un altro evento è già accaduto.

Il teorema di Bayes è basato sul concetto di probabilità condizionata, che misura la probabilità di un evento A, dato che l’evento B è già accaduto. La probabilità condizionata è denotata come P(A|B) e si legge “la probabilità di A dato B”.

Il Teorema di Bayes

Il Teorema di Bayes afferma che la probabilità di un evento A, dato che l’evento B è già accaduto, è uguale alla probabilità di B dato A moltiplicata per la probabilità di A, divisa per la probabilità di B:

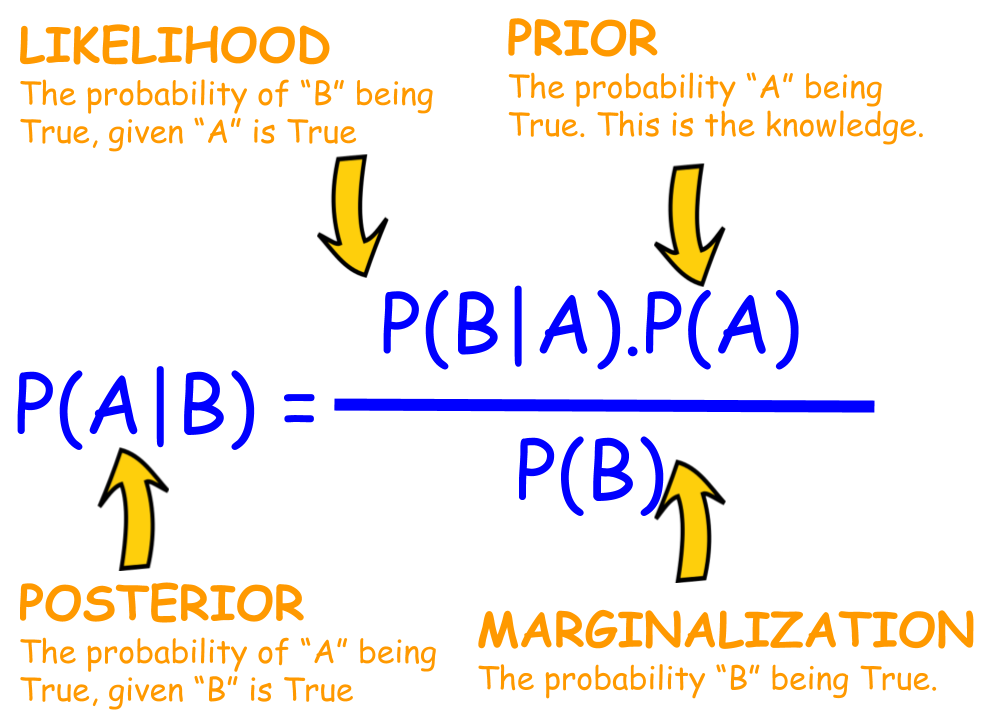
P(A|B) = [P(B|A) * P(A)] / P(B)

Dove:

* P(A|B) è la probabilità di A dato B
* P(B|A) è la probabilità di B dato A
* P(A) è la probabilità di A
* P(B) è la probabilità di B

Un Esempio Concreto

Immaginiamo di avere un test medico per una malattia che ha un’accuratezza del 90%. Questo significa che il test restituisce un risultato positivo nel 90% dei casi in cui la malattia è presente, e un risultato negativo nel 90% dei casi in cui la malattia è assente. Sappiamo anche che la malattia è presente nell’1% della popolazione.

Ora, supponiamo che una persona faccia il test e riceva un risultato positivo. Qual è la probabilità che la persona abbia effettivamente la malattia?

Possiamo usare il Teorema di Bayes per rispondere a questa domanda.

* P(Malattia|Positivo) è la probabilità di avere la malattia dato un risultato positivo. Questa è la probabilità che stiamo cercando.
* P(Positivo|Malattia) è la probabilità di un risultato positivo dato che la malattia è presente. Questo è l’accuratezza del test, che è 0.9.
* P(Malattia) è la probabilità di avere la malattia. Questo è la prevalenza della malattia, che è 0.01.
* P(Positivo) è la probabilità di un risultato positivo. Questo può essere calcolato usando la legge della probabilità totale.

Applicando il Teorema di Bayes, otteniamo:

P(Malattia|Positivo) = [P(Positivo|Malattia) * P(Malattia)] / P(Positivo) = (0.9 * 0.01) / P(Positivo)

Per calcolare P(Positivo), dobbiamo considerare sia i casi in cui la malattia è presente che i casi in cui la malattia è assente:

P(Positivo) = P(Positivo|Malattia) * P(Malattia) + P(Positivo|Non Malattia) * P(Non Malattia) = (0.9 * 0.01) + (0.1 * 0.99) = 0.108

Sostituendo P(Positivo) nell’equazione precedente, otteniamo:

P(Malattia|Positivo) = (0.9 * 0.01) / 0.108 = 0.083

Quindi, la probabilità che una persona abbia la malattia dato un risultato positivo è circa l’8.3%. Questo dimostra come il Teorema di Bayes ci permette di aggiornare le nostre credenze sulla base di nuove informazioni.

Interpretazioni del Teorema di Bayes

Il Teorema di Bayes può essere interpretato in due modi principali:

* Interpretazione frequentista: In questa interpretazione, la probabilità è vista come la frequenza relativa di un evento in un numero infinito di prove.
* Interpretazione bayesiana: In questa interpretazione, la probabilità è vista come un grado di fiducia in un evento.

L’interpretazione bayesiana è particolarmente utile per aggiornare le nostre credenze sulla base di nuove informazioni. Questo perché ci permette di esprimere le nostre credenze iniziali come probabilità soggettive e di aggiornarle in base alle nuove evidenze.

Applicazioni del Teorema di Bayes

Il teorema di Bayes è un potente strumento che può essere applicato in una vasta gamma di campi, dalla medicina alla finanza, dall’intelligenza artificiale all’analisi dei dati. La sua capacità di aggiornare le probabilità sulla base di nuove informazioni lo rende particolarmente utile in situazioni incerte.

Applicazioni del Teorema di Bayes in vari campi

Il teorema di Bayes trova applicazioni pratiche in molti settori. Ecco alcuni esempi:

Medicina

• Diagnosi medica: Il teorema di Bayes può essere utilizzato per calcolare la probabilità che un paziente abbia una particolare malattia, dato un set di sintomi. Ad esempio, un medico potrebbe utilizzare il teorema di Bayes per determinare la probabilità che un paziente abbia il cancro al seno, dato che ha un nodulo al seno e altri sintomi.
• Screening medico: Il teorema di Bayes può essere utilizzato per valutare l’efficacia degli screening medici, come i test per il cancro al colon-retto. Questo aiuta a determinare se lo screening è efficace nel ridurre il rischio di morte per la malattia.

Finanza

• Gestione del rischio: Il teorema di Bayes può essere utilizzato per valutare il rischio di un investimento. Ad esempio, un gestore di fondi potrebbe utilizzare il teorema di Bayes per determinare la probabilità che un’azienda fallisca, dato il suo bilancio e altri fattori.
• Valutazione del credito: Le istituzioni finanziarie utilizzano il teorema di Bayes per valutare il rischio di credito di un mutuatario. Questo aiuta a determinare se concedere o meno un prestito e a quale tasso di interesse.

Intelligenza Artificiale

• Filtraggio dello spam: I filtri antispam utilizzano il teorema di Bayes per classificare le email come spam o non spam. Il teorema di Bayes aiuta a determinare la probabilità che un’email sia spam, dato il suo contenuto e altre caratteristiche.
• Riconoscimento di immagini: Il teorema di Bayes può essere utilizzato per classificare le immagini in base al loro contenuto. Ad esempio, un algoritmo di riconoscimento facciale potrebbe utilizzare il teorema di Bayes per determinare la probabilità che un’immagine mostri un particolare individuo.

Analisi dei dati

• Analisi predittiva: Il teorema di Bayes può essere utilizzato per creare modelli predittivi che possono essere utilizzati per prevedere eventi futuri. Ad esempio, un modello predittivo potrebbe essere utilizzato per prevedere la probabilità che un cliente acquisti un particolare prodotto.
• Rilevamento di anomalie: Il teorema di Bayes può essere utilizzato per identificare le anomalie nei dati. Ad esempio, un sistema di rilevamento delle frodi potrebbe utilizzare il teorema di Bayes per identificare le transazioni sospette.

Esempi concreti

Ecco una tabella che mostra le diverse applicazioni del teorema di Bayes con esempi concreti per ogni campo:

Campo	Esempio
Medicina	Un medico utilizza il teorema di Bayes per determinare la probabilità che un paziente abbia il cancro al seno, dato che ha un nodulo al seno e altri sintomi.
Finanza	Un gestore di fondi utilizza il teorema di Bayes per determinare la probabilità che un’azienda fallisca, dato il suo bilancio e altri fattori.
Intelligenza Artificiale	Un filtro antispam utilizza il teorema di Bayes per classificare le email come spam o non spam.
Analisi dei dati	Un modello predittivo utilizza il teorema di Bayes per prevedere la probabilità che un cliente acquisti un particolare prodotto.

Sfide e vantaggi dell’utilizzo del Teorema di Bayes

L’utilizzo del teorema di Bayes presenta sia sfide che vantaggi:

Sfide

• Determinazione delle probabilità a priori: Una delle sfide nell’utilizzo del teorema di Bayes è la determinazione delle probabilità a priori. Queste probabilità rappresentano la probabilità di un evento prima di ricevere nuove informazioni. La scelta di probabilità a priori accurate è fondamentale per ottenere risultati accurati.
• Quantità di dati: Il teorema di Bayes funziona meglio con grandi quantità di dati. Se la quantità di dati è limitata, le probabilità calcolate potrebbero non essere accurate.
• Interpretazione dei risultati: L’interpretazione dei risultati del teorema di Bayes può essere complessa, soprattutto per i non esperti di statistica.

Vantaggi

• Aggiornamento delle probabilità: Il teorema di Bayes consente di aggiornare le probabilità sulla base di nuove informazioni. Questo è un vantaggio significativo in situazioni incerte.
• Predizione degli eventi: Il teorema di Bayes può essere utilizzato per prevedere eventi futuri, come la probabilità che un cliente acquisti un prodotto.
• Decisioni basate sui dati: Il teorema di Bayes fornisce un quadro per prendere decisioni basate sui dati.

Modelli Bayesiani

I modelli bayesiani sono una classe di modelli statistici che utilizzano il teorema di Bayes per aggiornare le probabilità di eventi in base a nuove informazioni. Questi modelli sono particolarmente utili per affrontare problemi in cui l’incertezza è elevata e i dati sono limitati.

Tipi di modelli bayesiani

I modelli bayesiani possono essere classificati in diversi tipi, a seconda della loro struttura e del tipo di dati che analizzano. Tra i modelli più comuni troviamo:

• Modelli lineari bayesiani: Questi modelli estendono i modelli lineari tradizionali, incorporando informazioni a priori sulle variabili del modello. Sono utilizzati per modellare relazioni lineari tra variabili, tenendo conto dell’incertezza nei parametri del modello.
• Modelli gerarchici: Questi modelli sono utilizzati per analizzare dati strutturati, ad esempio dati raccolti da diversi gruppi o livelli di una gerarchia. Permettono di stimare parametri comuni a tutti i gruppi e parametri specifici per ciascun gruppo, tenendo conto della correlazione tra i gruppi.
• Modelli di rete bayesiana: Questi modelli rappresentano le relazioni di dipendenza tra variabili mediante un grafo. Ogni nodo del grafo rappresenta una variabile e gli archi rappresentano le dipendenze tra le variabili. I modelli di rete bayesiana sono utili per modellare sistemi complessi con molte variabili interdipendenti.

Utilizzo dei modelli bayesiani

I modelli bayesiani sono utilizzati per inferire le probabilità di eventi e per fare previsioni. Il processo di inferenza bayesiana consiste nell’aggiornare la distribuzione di probabilità a priori di un evento in base a nuove informazioni, ottenendo una distribuzione di probabilità a posteriori.

La probabilità a posteriori di un evento è proporzionale alla probabilità a priori dell’evento moltiplicata per la verosimiglianza dei dati osservati.

Le previsioni basate sui modelli bayesiani sono realizzate utilizzando la distribuzione a posteriori dei parametri del modello. Ad esempio, un modello bayesiano può essere utilizzato per prevedere il prezzo di un’azione in base ai dati storici del mercato e ad altre informazioni rilevanti.

Esempio di applicazione

Consideriamo un esempio pratico di come un modello bayesiano può essere utilizzato per risolvere un problema. Supponiamo di voler stimare la probabilità che un paziente abbia una certa malattia, dato che ha presentato alcuni sintomi specifici.

Un modello bayesiano può essere utilizzato per aggiornare la probabilità a priori della malattia, basata sulla prevalenza della malattia nella popolazione, in base ai sintomi osservati. La verosimiglianza dei sintomi, ovvero la probabilità di osservare quei sintomi dato che il paziente ha la malattia, può essere ottenuta da studi clinici o da dati storici.

Il modello bayesiano calcola quindi la probabilità a posteriori della malattia, tenendo conto sia della probabilità a priori che della verosimiglianza dei sintomi. Questo risultato può aiutare i medici a prendere decisioni più informate sul trattamento del paziente.

Bayesian statistics is all about using prior knowledge to update your beliefs based on new data. It’s like how you might adjust your opinion about a new restaurant based on reviews from friends. This kind of thinking is essential in tech, and you can see it in action in the story of mike lynch uk , who used Bayesian methods to build his successful tech company.

Understanding Bayesian concepts can help you make smarter decisions in a world filled with uncertainty.

Bayesian analysis is a powerful tool for making decisions in the face of uncertainty. It uses probability to update our beliefs about the world based on new evidence. For a deep dive into this revolutionary approach to data analysis, check out this article on Bayesian analysis.

The principles of Bayesian statistics can be applied in a wide range of fields, from medicine to finance to machine learning.